Bayesian Approach to Network Modularity
Abstract
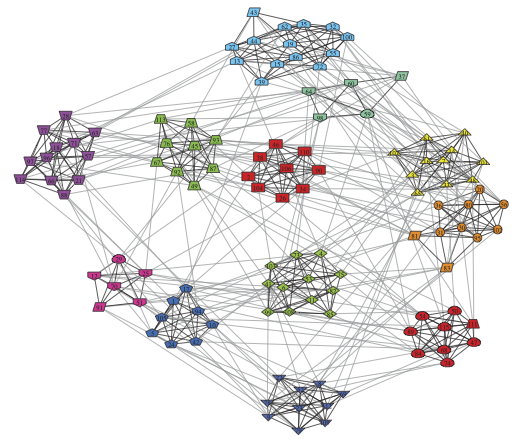
We present an efficient, principled, and interpretable technique for inferring module assignments and for identifying the optimal number of modules in a given network. We show how several existing methods for finding modules can be described as variant, special, or limiting cases of our work, and how the method overcomes the resolution limit problem, accurately recovering the true number of modules. Our approach is based on Bayesian methods for model selection which have been used with success for almost a century, implemented using a variational technique developed only in the past decade. We apply the technique to synthetic and real networks and outline how the method naturally allows selection among competing models.