Learning rates and states from biophysical time series: a Bayesian approach to model selection and single-molecule FRET data

Abstract

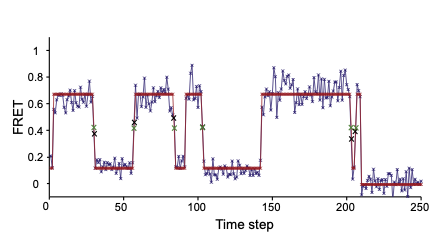
Time series data provided by single-molecule Förster resonance energy transfer (smFRET) experiments offer the opportunity to infer not only model parameters describing molecular complexes, e.g., rate constants, but also information about the model itself, e.g., the number of conformational states. Resolving whether such states exist or how many of them exist requires a careful approach to the problem of model selection, here meaning discrimination among models with differing numbers of states. The most straightforward approach to model selection generalizes the common idea of maximum likelihood—selecting the most likely parameter values—to maximum evidence: selecting the most likely model. In either case, such an inference presents a tremendous computational challenge, which we here address by exploiting an approximation technique termed variational Bayesian expectation maximization. We demonstrate how this technique can be applied to temporal data such as smFRET time series; show superior statistical consistency relative to the maximum likelihood approach; compare its performance on smFRET data generated from experiments on the ribosome; and illustrate how model selection in such probabilistic or generative modeling can facilitate analysis of closely related temporal data currently prevalent in biophysics. Source code used in this analysis, including a graphical user interface, is available open source via http://vbFRET.sourceforge.net .