Inferring relevant social networks from interpersonal communication

Abstract

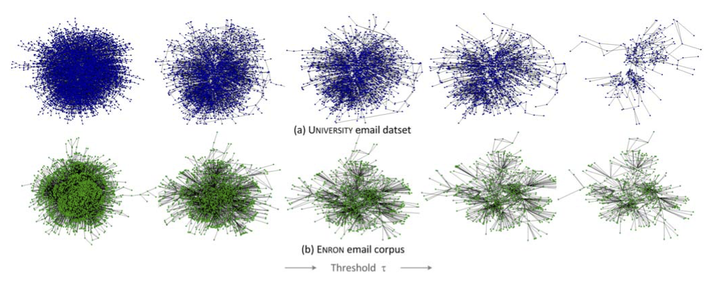
Researchers increasingly use electronic communication data to construct and study large social networks, effectively inferring unobserved ties (e.g. i is connected to j) from observed communication events (e.g. i emails j). Often overlooked, however, is the impact of tie definition on the corresponding network, and in turn the relevance of the inferred network to the research question of interest. Here we study the problem of network inference and relevance for two email data sets of different size and origin. In each case, we generate a family of networks parameterized by a threshold condition on the frequency of emails exchanged between pairs of individuals. After demonstrating that different choices of the threshold correspond to dramatically different network structures, we then formulate the relevance of these networks in terms of a series of prediction tasks that depend on various network features. In general, we find: a) that prediction accuracy is maximized over a non-trivial range of thresholds corresponding to 5-10 reciprocated emails per year; b) that for any prediction task, choosing the optimal value of the threshold yields a sizable (~30%) boost in accuracy over naive choices; and c) that the optimal threshold value appears to be (somewhat surprisingly) consistent across data sets and prediction tasks. We emphasize the practical utility in defining ties via their relevance to the prediction task(s) at hand and discuss implications of our empirical results.